Quiz 3 - Chemical Kinetics: Mechanisms | Chemical Kinetics: Mechanisms

A catalyst can alter the rate law of a reaction by introducing a new reaction pathway with a different mechanism. This new mechanism can have a different rate-determining step, which may change the rate law.

However, a catalyst does not make the overall reaction more exothermic or endothermic; it does not change the enthalpy of the reaction. The catalyst only affects the reaction rate by lowering the activation energy.

To solve this, we can use the Arrhenius equation in its logarithmic form:

Therefore,

Given:

• The rate constant increases by 63%, so $\frac{{\mathrm{k}}_2}{{\mathrm{k}}_1}$ = 1.63
• T₁ = 40 + 273.15 = 313.15 K
• T₂ = 45 + 273.15 = 318.15 K

ln (1.63) = $\frac{{\mathrm{E}}_{\mathrm{a}}}{8.314}$ $\left(\frac{1}{313.15} - \frac{1}{318.15}\right)$ ⇒ 0.489 = E_a x 6.036 x 10^-6

E_a = 80.9 x 10³ J.mol^-1 = 80.9 kJ.mol^-1

To solve this, we can use the Arrhenius equation in its logarithmic form:

Therefore,

Given:

• T₁ = 37 + 273.15 = 310.15 K
• T₂ = 15 + 273.15 = 288.15 K

ln $\left(\frac{{\mathrm{k}}_2}{{\mathrm{k}}_1}\right)$ = $\frac{87000}{8.314}$ $\left(\frac{1}{310.15} - \frac{1}{288.15}\right)$ = -2.576

$\frac{{\mathrm{k}}_2}{{\mathrm{k}}_1}$ = e^-2.576 = $\frac{1}{13}$

The rate-determining step (slow step) in the mechanism is: Cl (g) + CHCl₃ (g) → HCl (g) + CCl₃ (g)

The rate law for the reaction is determined by the slowest step. According to the mechanism, the rate of the reaction should be proportional to the concentration of Cl and CHCl₃​: Rate = k [Cl][CHCl₃]

However, Cl is not a reactant but an intermediate, and its concentration must be expressed in terms of the initial reactants. From the fast equilibrium step: Cl₂ (g) → 2 Cl (g), the concentration of Cl can be related to [Cl₂] as: [Cl] ∝ [Cl₂].

Thus, the rate law becomes: Rate = k [Cl₂]^1/2[CHCl₃]

For the given rate law, Rate = k [H₂][NO]^₂, the mechanism must produce a rate law consistent with this expression.

• Step 1: 2 NO ⇌ N₂O₂​ is a fast equilibrium step, so the concentration of N₂O₂​ can be expressed in terms of [NO]².

• Step 2: If this step is slow, it will be the rate-determining step. The rate of this step would depend on the concentrations of N₂O₂ and H₂, leading to the rate law Rate = k [N₂O₂][H₂]. Since [N₂O₂] is proportional to [NO]², the rate law becomes Rate = k [H₂][NO]², which matches the given rate law.

Therefore, the mechanism could be consistent with the observed rate law if step 2 is the slow, rate-determining step.

According to the Arrhenius equation:

By measuring the rate constant k at different temperatures and plotting lnk versus T^-1 (a plot called an Arrhenius plot), a straight line is obtained with a slope of - $\frac{{\mathrm{E}}_{\mathrm{a}}}{\mathrm{R}}$ and an intercept of lnA.

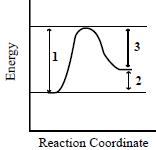
In the energy-reaction coordinate diagram:

• Dimension 1 represents the activation energy (the energy barrier that must be overcome for the reaction to proceed).
• Dimension 2 represents the difference in energy between the reactants and products (which is the enthalpy change, ΔH).
• Dimension 3 likely represents the energy difference between the activated complex (transition state) and the products.

When a catalyst is added:

• Dimension 1 (activation energy) decreases because the catalyst provides an alternative pathway with a lower activation energy.
• Dimension 2 (enthalpy change, ΔH) does not change because the catalyst does not affect the energy difference between the reactants and products.
• Dimension 3 (the difference between the transition state and products) is related to the activation energy, so it may also change depending on how the reaction pathway is altered by the catalyst.

According to the Arrhenius equation:

By measuring the rate constant k at different temperatures and plotting lnk versus T^-1 (a plot called an Arrhenius plot), a straight line is obtained with a slope of - $\frac{{\mathrm{E}}_{\mathrm{a}}}{\mathrm{R}}$.